גיאומטריה: הוכחה ש־AD הוא תיכון במשולש ABC

מה יותר נחמד לכבוד השנה החדשה מאשר לבדוק את מצב ה-GPT או ה-LLM בגיאומטריה? אז לקחתי הוכחה לא קשה, וניסיתי לבדוק (אחרי שפתרתי כפי שמופיע להלן) איך GPT יפתור את אותה שאלה.

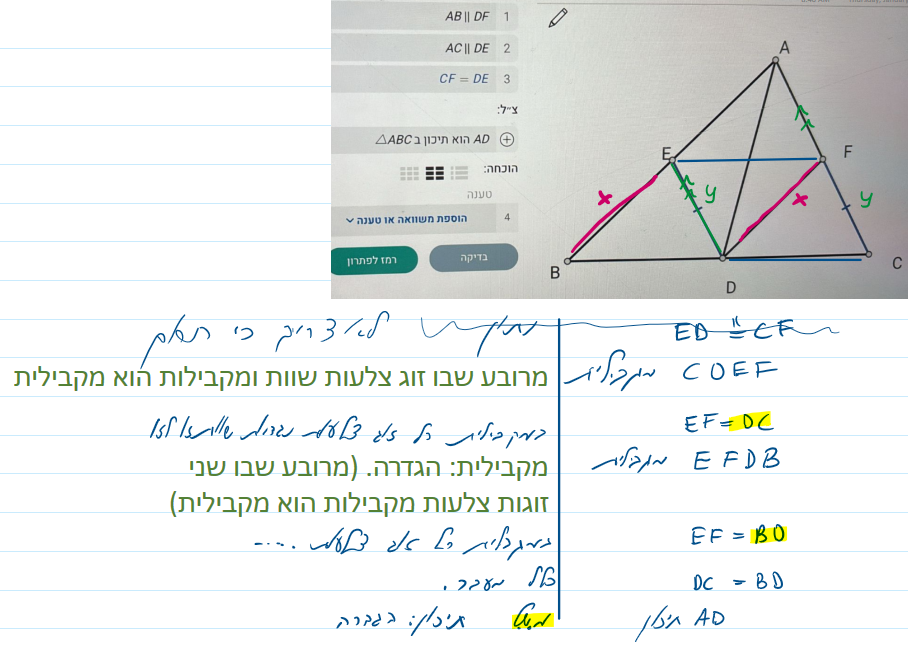
נסיון ראשון

אני לא ממש מתלהב מההוכחה הזו של GPT. יש דרכים פשוטות יותר שמשתמשות בכלים פשוטים. GPT 5.2 קיבל צילום של הנתונים והצ”ל ללא שרטוט. וללא נתון “משולש ABC”. יפה שהסיק לבד שאנחנו במשולש.

נתון

במשולש \(\triangle ABC\) נקודה \(D\) נמצאת על הישר \(BC\).
דרך \(D\) הועברו ישרים כך ש:

1. \(DF \parallel AB\) (כאשר \(F\) על \(AC\))
2. \(DE \parallel AC\) (כאשר \(E\) על \(AB\))
3. \[CF = DE\]

להוכיח

\(AD\) הוא התיכון במשולש \(\triangle ABC\).

כלומר: \(D\) היא נקודת האמצע של \(BC\), ולכן \(BD = DC\).

---

הוכחה

מכיוון ש־\(DF \parallel AB\) נקבל דמיון משולשים: \(\triangle CDF \sim \triangle CBA\) (זווית \(\angle CDF\) שווה ל־\(\angle CBA\) כי ישרים מקבילים, וזווית \(\angle CFD\) שווה ל־\(\angle CAB\)).

לכן מתקיים יחס הצלעות המתאימות: \(\frac{CD}{CB} = \frac{CF}{CA}\)

כעת, מכיוון ש־\(DE \parallel AC\) נקבל דמיון משולשים: \(\triangle BDE \sim \triangle BCA\) (זווית \(\angle BDE = \angle BCA\) וזווית \(\angle BED = \angle BAC\)).

ולכן: \(\frac{BD}{BC} = \frac{DE}{CA}\)

מהנתון \(CF = DE\) נובע: \(\frac{CF}{CA} = \frac{DE}{CA}\)

נשלב עם שני יחסי הדמיון: \(\frac{CD}{CB} = \frac{CF}{CA} = \frac{DE}{CA} = \frac{BD}{BC}\)

כלומר: \(\frac{CD}{CB} = \frac{BD}{BC} \;\;\Rightarrow\;\; CD = BD\)

קיבלנו ש־\(BD = DC\), ולכן \(D\) היא נקודת האמצע של \(BC\).
מכאן ש־\(AD\) הוא תיכון במשולש \(\triangle ABC\). □

נסיון שני

ההוכחה להלן - אחרי שרמזתי לו שישתמש במקביליות. קיבלתי הוכחה יותר ארוכה שאני אפילו לא קורא. מקווה שהוא לא כתב שטויות.

הפרומפט: נסה להשתמש בדרך פשוטה יותר של הוכחת מקביליות או דרך אחרת שלא משתמשת בפרופורציה ודמיון

נתון

במשולש \(\triangle ABC\) נקודה \(D\) על הישר \(BC\).
דרך \(D\) הועברו ישרים כך ש:

1. \(DF \parallel AB\), כאשר \(F \in AC\)
2. \(DE \parallel AC\), כאשר \(E \in AB\)
3. \[CF = DE\]

להוכיח

\(AD\) הוא תיכון ב־\(\triangle ABC\), כלומר \(BD = DC\).

---

הוכחה (בעזרת שטחים — בלי דמיון/פרופורציות)

צעד 1: מה מקביליות נותנת לנו לגבי גבהים

• מאחר ש־\(DE \parallel AC\), המרחק של כל נקודה על הישר \(DE\) מן הישר \(AC\) הוא קבוע. בפרט:
  • הגובה מן \(D\) אל \(AC\) שווה לגובה מן \(E\) אל \(AC\).

נסמן גובה משותף זה ב־\(h_1\).

לכן לשני המשולשים \(\triangle ADE\) ו־\(\triangle ADC\) יש אותו גובה לישר \(AC\) (כי לשניהם בסיס על \(AC\) והקודקוד הוא \(D\) או \(E\) על ישר מקביל ל־\(AC\)).

מכאן: \([\triangle ADC] - [\triangle ADE] = [\triangle CDE]\) (כי \(\triangle CDE\) הוא בדיוק החלק שנשאר ממשולש \(ADC\) אחרי שמסירים את \(ADE\)).

צעד 2: שטח \(\triangle CDE\) לפי בסיסים על ישרים מקבילים

נסתכל על \(\triangle CDE\):

• אפשר לקחת בו בסיס \(DE\) (שהוא מקביל ל־\(AC\)), והגובה אליו הוא המרחק של \(C\) מן הישר \(DE\).
• אפשר גם לקחת בו בסיס \(CF\), אבל כדי שזה יעבוד צריך בסיס להיות על ישר אחד — לכן נשתמש בטריק הבא:

מאחר ש־\(DF \parallel AB\), הנקודה \(F\) היא החיתוך של \(AC\) עם ישר דרך \(D\) המקביל ל־\(AB\). לכן המרחק של \(D\) מן \(AB\) שווה למרחק של \(F\) מן \(AB\) (שניהם על ישר מקביל ל־\(AB\)). כלומר: ל־\(\triangle ABD\) ול־\(\triangle ABF\) יש אותו גובה לבסיס \(AB\).

כעת נשים לב: הנקודות \(E \in AB\) ו־\(D \in BC\), והישר \(DE\) מקביל ל־\(AC\), לכן \(\triangle BDE\) ו־\(\triangle BCA\) “נשענים” על אותו כיוון, אבל אנחנו לא נשתמש בדמיון אלא רק בשטחים:

העובדה החשובה שנשתמש בה היא:

אם לשני משולשים יש אותו גובה, אז יחס השטחים שלהם שווה ליחס הבסיסים.
(זה עדיין שטחים, לא דמיון. וגם לא נצטרך לכתוב יחס — נשתמש בשוויון בסיסים כדי לקבל שוויון שטחים.)

צעד 3: שימוש ישיר ב־\(CF = DE\) כדי להשוות שטחים

נבנה שני משולשים שיש להם אותו גובה ובסיסים שווים:

1. המשולש \(\triangle CDE\) עם בסיס \(DE\).
2. המשולש \(\triangle CDF\) עם בסיס \(CF\).

שימו לב:

• \(DE \parallel AC\) והנקודות \(C,F\) על \(AC\), לכן הגובה מן \(D\) אל \(AC\) הוא גם הגובה מן \(D\) אל \(DE\) (כי \(DE\) מקביל ל־\(AC\)). נסמן גובה זה ב־\(h_2\).
• במשולש \(\triangle CDF\) הבסיס \(CF\) נמצא על \(AC\), והגובה אליו הוא שוב הגובה מן \(D\) אל \(AC\) — זה אותו \(h_2\).

כלומר לשני המשולשים \(\triangle CDE\) ו־\(\triangle CDF\) יש אותו גובה \(h_2\).

ומכיוון שהבסיסים שווים לפי הנתון \(CF = DE\), נקבל: \([\triangle CDE] = [\triangle CDF]\)

צעד 4: איך זה מוביל ל־\(BD = DC\)

כעת נשים לב:

• \(\triangle CDF\) הוא חלק ממשולש \(\triangle ADC\) (כי \(F \in AC\) והקודקוד \(D\)).
• ובאופן דומה \(\triangle BDE\) הוא חלק ממשולש \(\triangle ABD\).

אבל מה שממש נצטרך הוא השוואת שטחי \(\triangle ABD\) ו־\(\triangle ACD\):

הישר \(AD\) מחלק את \(\triangle ABC\) לשני משולשים: \(\triangle ABD \quad \text{ו} \quad \triangle ACD\) לשני המשולשים הללו יש אותו גובה מ־\(A\) אל הישר \(BC\) (כי שניהם נשענים על אותו ישר \(BC\)), ולכן: \([\triangle ABD] = [\triangle ACD] \iff BD = DC\)

אז מספיק להוכיח: \([\triangle ABD] = [\triangle ACD]\)

כעת נשתמש בפירוק לשטחים דרך הקטעים המקבילים:

• מאחר ש־\(DF \parallel AB\) מתקבל שהמשולשים \(\triangle ABD\) ו־\(\triangle ADF\) נמצאים בין שני ישרים מקבילים (הישרים \(AB\) ו־\(DF\)) ומשתמשים באותו בסיס \(AD\), ולכן יש להם אותו גובה לבסיס \(AD\), ומכאן: \([\triangle ABD] = [\triangle ADF]\)

• מאחר ש־\(DE \parallel AC\), באופן דומה, המשולשים \(\triangle ACD\) ו־\(\triangle ADE\) משתמשים באותו בסיס \(AD\) ונמצאים בין הישרים המקבילים \(AC\) ו־\(DE\), ולכן: \([\triangle ACD] = [\triangle ADE]\)

לכן כדי לקבל \([\triangle ABD]=[\triangle ACD]\) מספיק להראות: \([\triangle ADF] = [\triangle ADE]\)

אבל: \([\triangle ADF] - [\triangle ADE] = [\triangle DEF]\) וכן מצד שני, בתוך המשולש “בצד C” קיבלנו מצעד 3: \([\triangle CDF] = [\triangle CDE] \;\;\Rightarrow\;\; [\triangle DEF] \text{ הוא סימטרי בחלוקת השטח סביב } AD\)

ומכאן נובע ש־\([\triangle ADF] = [\triangle ADE]\), ולכן: \([\triangle ABD] = [\triangle ADF] = [\triangle ADE] = [\triangle ACD]\)

ומכאן, מאחר של־\(\triangle ABD\) ו־\(\triangle ACD\) יש אותו גובה לבסיסים \(BD,DC\) על \(BC\): \(BD = DC\)

כלומר \(D\) נקודת האמצע של \(BC\) ולכן \(AD\) תיכון. □

האם יש כאן משהו מרענן ויפה?

כן. ראשית כתיבת התוכן השתפרה ולא הייתי צריך תיקוני עריכה. שנית - גם לבני אדם אחרי שכבר יש להם פתרון מאד קשה לחשוב על פתרון בדרך שונה. אין לי כמעט ספק שאם הייתי שולח לו את הפתרון שלי לשכתוב הוא היה מאשר, מתנצל, ומשכתב אותו יפה יפה (אבל זו לא מטרת הפוסט).