🔢 קשר בין פולינום לגרף | מתמטיקה עם גיא

מטרות ומדיה

🎯 מטרות השיעור

תלמידים יבינו שפונקציה פולינומית הנתונה כמכפלת גורמים מתאפסת כאשר אחד הגורמים מתאפס.
יכירו את שיטת “הנחש” ככלי לשרטוט גרף של פולינום לפי שורשיו וסימן הפונקציה.
ישפרו שפה מתמטית (כתיבת גרירות לנק’ אפס, ורישום טבלאי שיעזור בהמשך לטבלאות סיווג קיצון)
(בהתאם למה שיוגדר, ולקצב) ילמדו לפעול גם בכיוון ההפוך: מגרף לפונקציה.

מדיה

רוב השיעור יועבר על הלוח בטוש

הכנתי Geogebra להערכתי לא יהיה צורך. אני מכוון לשיעור קצת יותר איטי כדי שיוכלו לעקוב ולרשום.

המערך מאפשר גם הקרנה על הלוח או למידה עצמית (זה לא התכנון)

🧱 שלבי השיעור

1. פתיחה – חזרה קצרה והצגת הנושא

מה קורה כשכופלים $5 \cdot0 = ? \\ 5\cdot0\cdot3 = ?$

איך מציירים את $?f(x)=(x+1)(x-2)$

ומה אם יש 3 גורמים?

על מה אפשר להסכים כרגע?

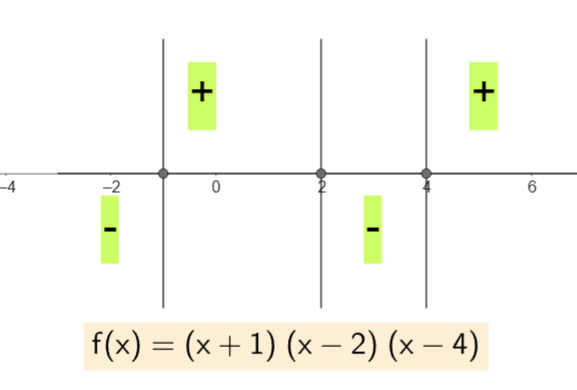
אם פונקציה נתונה בצורה של מכפלת גורמים, לדוגמה: $f(x) = (x+1)(x-2)(x-4)$
אז כל ערך שיגרום לאחד הגורמים להתאפס – יגרום לפונקציה להתאפס.

2. הדגמה: מה קורה כשכופלים באפס?

שאלות:

מה קורה לביטוי $(x+1)(x-2)$ כאשר $x = 2$?
ומה כאשר $? x = -1$

דגש: $x=+2$ חיובי כשבסוגריים יש מינוס

$(x+1) = 0 ⟹ \boxed{x = -1}$ שלילי כשבסוגריים יש פלוס

לסיכום: הפונקציה מתאפסת בכל מקום בו אחד הגורמים מתאפס.

הערה למקרה שתלמידים פותחים סוגריים

למרות שאנחנו רגילים לפתוח סוגרים - ככל שיעבור הזמן יהיו יותר מקרים בהם נרצה לעשות ההפך. ברוב המקרים נעדיף יצוג של מכפלת גורמים. כנראה שלא אכנס לזה

3. שיטת הנחש 🐍 – הסבר ותרגול

כיצד נשרטט את הגרף הבא? $\quad \quad f(x) \quad = \underset{\downarrow}{(x+1)}\underset{\downarrow}{(x-2)}\underset{\downarrow}{(x-4)} \\ f(x)=0 ⟹ x=-1, x=2, x=4$

פירוט הצבות

$f(-3) = -70 < 0 ⟹ - \\ f(0) = 8 > 0 ⟹ + \\ f(3) = -4 < 0 ⟹ - \\ f(6) = 56 > 0 ⟹ +$

נחש

	$+$		$+$
$\quad-$		$-$

תחום חיוביות

\[-1 < x < 2,\quad x > 4\]

למורה

סיכום מפורט - השלבים בשיטת הנחש:

מוצאים את השורשים של הפונקציה (כל ערך שמאפס גורם במכפלה).
מחלקים את ציר ה־ $x$ לתחומים לפי השורשים (נקודות האפס).
מחשבים את סימן הפונקציה בכל תחום ומסמנים חיוביות מעל ושליליות מתחת לציר. דגש: מתייחסים ל- $y$. מה שמבדיל בין חיובי לשלילי הוא ציר ה-x.
סרטוט נחש (הפולינום) על ידי חיבור הנקודות.

רישום לוח מוצע:

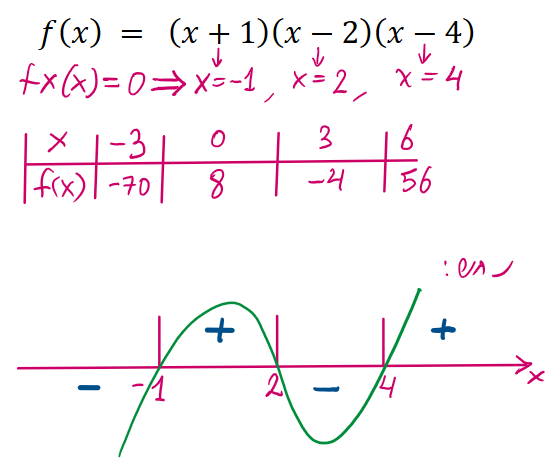
רישום לוח

שלבי שיטת הנחש

מוצאים נקודות שמאפסות $y=0$
מסמנים על הציר
מחשבים סימנים
± על הציר
נחש (חיבור נקודות)

מסקנות:

הפונקציה מתאפסת ב־ $x = -2,\ 1,\ 4$
בכל תחום בין השורשים היא שומרת על סימן קבוע. למה?

עבור 3 נקודות 0 צריך 4 בדיקות סימן

חשוב לוודא שאין תוספת קבוע שמחובר למכפלה ומזיז אותה מעלה. במקרה כזה הכל משתנה. להדגים על גרף מוזז

הרחבה לגבי הזזה אם יש זמן

ניתן להדגים שמציאת נקודות התאפסות ללא ההזזה, מאפשרת להסיק מסקנות על הפונקציה המוזזת

🧪 ביחד: תרגול לכיתה

.שאלה 1. מצאו את שורשי הפונקציות הבאות ושרטטו לפי שיטת הנחש:

אשאל אותם ונכתוב יחד פונקציות

א. $f(x) = (x-10)(x+7)(5-x)$

נחש

$\quad+$		$+$
	$-$		$-$

ב. $f(x) = (x-10)(x+7)(x-5)$

נחש

	$+$		$+$
$\quad-$		$-$

שאלה לתלמידים : אז למה בעצם מסביב לכל שורש מתחלף הסימן?

שאלה 2. אתגר – שורש כפול

נתונה $$ f(x) = (x-10)(x+7)(x-5)(x-5)

א. מה קורה ב־ $\ x = -1$?

ב. כיצד נראית הפונקציה באזור זה?

הפונקציה לא תמיד מזגזגת סביב נקודות ההתאפסות. הנחש מתמודד גם עם המקרים האלו

ג. מדוע הגרף “נוגע” בציר במקום לחצות?

🧪 תרגול נוסף

\[f(x)=(x−2)(x−4)(x−6)\]
$f(x)=(x−2)(4-x)(x−6)$ היפוך הסדר בין המספרים - למה זה שקול?.
\[f(x)=x^3(x−2)\]

מגרף לאלגברי ועוד

שאלה 3 מגרף לבחירת הייצוג האלגברי

על בסיס זמן פנוי. לברר עם א’ או א’ אם למדו את זה או שגם זה חדש

גרסה שאני מעדיף:

כנראה שבמקום הגרף הזה, אצייר על הלוח סקיצה של פולינום ממעלה שלישית עם 3 חיתוכים כגון $(x+1)(x-1)(x-3)$ וננסה לבנות ביחד פונצקיה. אחרי שנבנה אות הפולינום, אצייר שיקוף ביחס לציר $y$ ואשאל איך ניתן לקבל צורה כזו.

גרסה חלופית -בחירה בין פונקציות

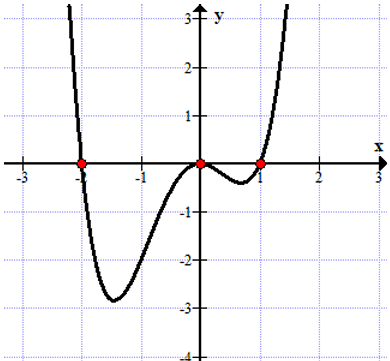
הסתכלו על הגרף הבא: נתון הגרף הבא

הגרף מתאר פולינום המתאפס בשלוש נקודות:
$x = -2,\ x = 0,\ x = 1$

שתי פונקציות מוצעות:

\[f(x) = x^2(x+2)(x-1)\]
\[g(x) = x(x+2)(x-1)\]

❓ איזו מבין השתיים מתאימה לגרף?

💡 רמז – נסו להציב ערך כלשהו

בואו נציב $x = -1$ בשתי הפונקציות:

\[f(-1) = (-1)^2 \cdot (1) \cdot (-2) = \\ = 1 \cdot 1 \cdot (-2) = -2 \\ g(-1) = (-1) \cdot (1) \cdot (-2) = 2\]

בגרף נראה כי בנקודה $x = -1$ הפונקציה נמצאות מתחת לציר ה־x, ולכן ערכה שלילי.
רק הפונקציה $f(x)$ מתאימה להתנהגות זו.

🔍5. נושא מתקדם- נוותר על זה – מעלת הפולינום

רק אם נותר זמן, ניתן לעסוק גם בקשר בין מספר הגורמים למעלת הפולינום:

אם כל גורם ממעלה ראשונה, אז מספר הגורמים = מעלת הפולינום. לדוגמה: $f(x) = (x-2)(x+3)(x-1) \\ \Rightarrow \text{מעלה 3}$

🧠6. (לא מעריך שיהיה זמן. ואני לא רוצה להתפזר) שאלות פתוחות למחשבה

האם כל פונקציה פולינומית מתאפסת?
האם תמיד ניתן לכתוב פונקציה פולינומית כמכפלת גורמים?
מה קורה אם לפולינום אין שורשים ממשיים?
כיצד ניתן להסיק על מספר השורשים מתוך צורת הפונקציה?

Geogebra ישאר לסוף - רק אם אראה בזה תועלת מעבר ללוח

להערכתי הכי נכון בסופו של דבר יהיה לעבוד ידני לגמרי על פולינום ממספרים שהתלמידים יגדירו בכל פעם. less is more.. כאן אשרטט את הציר, ואסביר את שיטת הנחש.

⬅ מעבר לגאוגברה